|
Learning objectives of this
article:
-
Define a explain the present value of an
annuity.
-
How is it calculated?
-
What are the benefits of its calculation?
Contents:
The present value of an annuity is
an amount of money today which is equivalent to a
series of equal payments in the future. For example,
you have won a lottery and lottery officials give
you the choice of having a lump-sum payment today or
a series of payments at the end of each of the next
5 years. The two alternatives would be considered
equivalent (in a monetary sense) if by investing the
lump-sum today you could generate (with accumulated
interest) annual withdrawal equal to five
installments offered by the lottery. An assumption
is that the final withdrawal would deplete the
investment completely. Consider the following
example.
Following formula is use for the calculation of
present value of an annuity:
|
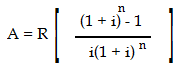
- R = Amount of an annuity
- i = interest rate per
compounding period
- n = Number of annuity payments
(also, the number of compounding
periods)
- Present value of the annuity
|
A person recently won a state lottery. The terms
of the lottery are that the winner will receive
annual payments of $20,000 at the end of this year
and each of the following 3 years. If the winner
could invest money today at the rate of 8 percent
per year compounded annually, what is the present
value of the four payments?
Solution:
There are problems in which we may be given the
present value of an annuity and need to determine
the size of the corresponding annuity. For example,
given a loan of $10,000 which is received today,
what quarterly payments must be made to repay the
loan in 5 years if interest is charged at the rate
of 10 percent per year, compounded quarterly? The
process of repaying loan by installment payments is
referred to as amortizing a loan.
To determine the size of an annuity, the formula
is solved for R:
The quarterly payment necessary to repay the
above motioned $10,000 is calculated as
follows:
|